成都大学“专升本”高等数学考试大纲

6.会求空间曲线的切线和法平面方程(仅限参数方程情形)，会求空间曲面的切平面和法线方程.

7.会求二元函数的极值.会用拉格朗日乘数法求解实际问题的最值.

(二)二重积分

1.了解二重积分的概念，理解二重积分的几何意义，掌握二重积分的性质.

2.熟练掌握二重积分在直角坐标系和极坐标系下的计算方法，会交换二次积分的积分次序.

3.会用二重积分计算空间立体的体积.

六、无穷级数

(一)数项级数

1.理解级数收敛、发散的概念.了解级数的基本性质，掌握级数收敛的必要条件.

2.掌握正项级数的比较判别法、比值判别法和根值判别法.

3.掌握几何级数、调和级数、 p 级数的敛散性.

4.会用莱布尼茨判别法.

5.理解级数绝对收敛与条件收敛的概念，会判断级数的绝对收敛与条件收敛.

(二)幂级数

1.了解幂级数的概念.会求幂级数的收敛半径、收敛区间(不要求讨论端点).

2.掌握幂级数在其收敛区间内的逐项求导、逐项积分的性质与方法，会求幂级数的和函数及收敛区间.

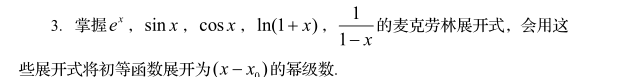
七、常微分方程

(一)一阶微分方程

1.了解微分方程的有关概念.

2.掌握可分离变量微分方程的解法.

3.了解齐次微分方程的解法.

4.掌握一阶线性微分方程的解法.

(二)二阶线性微分方程

1.了解二阶线性微分方程解的结构.

2.掌握二阶常系数齐次线性微分方程的解法.

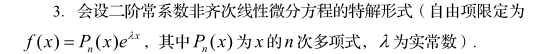
(一)行列式

1.了解行列式的概念，掌握行列式的性质.

2.掌握行列式按行(列)展开定理.

(二)矩阵

1.了解矩阵的概念.

2.熟练掌握矩阵的线性运算、乘法、转置、方阵的行列式及其运算性质.

3.理解逆矩阵的概念，掌握逆矩阵的性质.

4.理解伴随矩阵的概念，掌握伴随矩阵的性质，会用伴随矩阵求矩阵的逆矩阵.

5.掌握矩阵可逆的充分必要条件.

6.理解矩阵秩的概念，熟练掌握用初等变换法求矩阵的秩和逆矩阵.

7.会解矩阵方程.

(三)向量

1.了解 n 维向量的概念，理解向量的线性组合与线性表示.

2.理解向量组线性相关与线性无关的定义，掌握向量组线性相关性的判别方法.

3.理解向量组的极大线性无关组和向量组的秩的概念.

(四)线性方程组

1.掌握克莱姆法则.

2.理解齐次线性方程组有非零解的充分必要条件，理解齐次线性方程组的基础解系、通解的概念.

3.理解非齐次线性方程组有解的充分必要条件，理解非齐次线性方程组解的结构及通解的概念.

4.熟练掌握用矩阵的初等变换法求线性方程组的解.

Ⅳ.考试形式与试卷结构

一、考试形式

考试采用闭卷、笔试形式.试卷满分 150 分，考试时间 120 分钟.

二、试卷结构

1.考试题型可采用：判断题、单选题、填空题、计算题、解答题、证明题、应用题等形式.

2.试题按其难度分为：容易题、较易题、中等难度题、较难题.四种难度的试题应控制合适的分值比例，试卷总体难度适中.

3.试卷内容结构：线性代数约占 20%，其他内容约占 80%.

【参考书目】

1.同济大学数学系.高等数学(第七版).高等教育出版社.

2.同济大学数学系.工程数学：线性代数(第六版).高等教育出版社.

　　感谢您阅读成都大学“专升本”高等数学考试大纲，本文出自：诚为径统招专升本网，转载需带上本文链接地址：https://tzzsb.cwjedu.com/ksjc/21112/p2