2023年怀化学院专升本电气工程及其自动化《高等数学》课程考试大纲

《高等数学》课程考试大纲

一、课程基本信息

1.课程性质：公共基础课

2.适用对象：怀化学院专升本考生

二、课程考试目的

《高等数学》课程考试旨在考察学生对高等数学知识的掌握情况以及运用高等数学知识解决实际问题的能力.

三、考试内容与要求

第一章 函数极限与连续

(一)考试内容

一元函数的概念，函数的性质(有界性、单调性、奇偶性、周期性)，反函数，基本初等函数的概念、性质及其图形，复合函数，初等函数，数列极限，函数极限，无穷小与无穷大，无穷小与极限之间的关系，无穷小与无穷大之间的关系，极限的运算法则，极限存在准则，两个重要极限，无穷小的比较，函数的连续性，函数的间断点及其类型，连续函数的运算定理，初等函数的连续性，闭区间上连续函数的基本性质.

(二)考试要求

1.理解函数、初等函数的概念;

2.了解函数的性质以及反函数的概念;

3.掌握基本初等函数的性质及其图形;

4.理解极限的概念，思想方法;

5.了解极限的

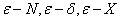
定义;

6.掌握左、右极限的概念，左、右极限与双边极限的关系;

7.掌握极限四则运算法则;

8.了解两个极限存在准则，熟练掌握两个重要极限;

9.理解无穷小的概念及与极限的关系;

10.了解无穷小的比较;

11.理解连续的两种定义，掌握连续性的证明方法、连续函数的运算性质，会判定间断点的类型;

12.了解闭区间上连续函数的性质，会用零点定理判别方程的根。

第二章 导数与微分

(一)考试内容

导数的概念，基本初等函数的导数，函数的和，差、积、商的导数，反函数和复合函数的导数，高阶导数，由隐函数、参数方程确定的函数的导数，微分的基本公式，微分形式不变性，微分在近似计算中的应用.

(二)考试要求

1.理解导数的概念，掌握利用概念求某些特殊极限的方法;

2.掌握导数的几何意义，掌握求切线和法线方程的方法，明确可导与连续的关系;

2.熟练掌握导数的运算;

3.理解微分的概念、几何意义、微分形式不变性，明确可导与可微的关系;

4.掌握微分在近似计算中的应用;

第三章 中值定理与导数的应用。

(一)考试内容

微分中值定理(罗尔定理、拉格朗日中值定理、柯西中值定理)，罗必塔法则，泰勒公式，函数单调性的判别、函数的凸凹性及拐点的判别、函数的极值概念及求法，最大值与最小值及其应用，函数图形的水平渐近线与铅直渐近线，函数作图.

(二)考试要求

1.了解三个微分中值定理的条件、结论，能证明前两个定理，了解构造函数的方法，掌握不等式的证明;

2.掌握洛必达法则的条件，结论以及常见的各种未定式的计算;

3.掌握泰勒公式和麦克劳林公式展开某些较简单的初等函数并求其近似值;

4.掌握函数的单调、凹凸、拐点、极值的判别,会求函数的单调区间、最值;

5.掌握解决简单的最大值、最小值的实际应用问题。

第四章 不定积分

(一)考试内容

原函数与不定积分的概念，不定积分的基本性质，积分基本公式，换元积分法，分部积分法，有理函数的积分，三角函数有理式的积分，简单无理函数的积分.

(二)考试要求

1.理解不定积分的概念，了解不定积分的几何意义;

2.熟练掌握不定积分的基本公式，掌握不定积分的性质;

3.熟练掌握不定积分的两类换元积分和分部积分法;

4.掌握较简单的有理函数、三角函数有理式的积分;

5.会求较简单的无理函数的积分;

第五章 定积分及其应用

(一)考试内容

定积分的概念，定积分的基本性质、微积分基本定理，定积分的换元积分及分部积分法，定积分的应用(求面积、体积、功、水压力).

(二)考试要求

1.理解定积分的概念，几何意义，掌握定积分的性质;

2.熟练掌握定积分的换元积分法和分部积分法;

3.理解变上限的定积分作为其上限的函数及其求导定理，熟悉牛顿-莱布尼兹公式和变上限积分函数的求导;

4.掌握定积分的微元法，掌握用定积分来表达面积、体积、弧长，了解功、水压力;

第六章 空间解析几何与向量代数

(一)考试内容

空间直角坐标系，两点间距离公式，向量代数，直线、平面的方程，常见曲面及其方程.

(二)考试要求

1.了解空间直角坐标系，建立空间点与数组的一一对应关系;

2.掌握两点间距离公式,了解向量的运算(线性运算、点乘法、叉乘法),两个向量夹角的求法与垂直、平行的条件;

3.熟练掌握用坐标表达式进行向量运算;

4.掌握平面，直线的方程;

5.知道常见曲面及其方程。

第七章 多元函数微分法及其应用

(一)考试内容

二元函数的概念，二元函数的图形，二元函数的极限、连续，偏导数的概念，高阶偏导数、全增量与全微分，全微分存在的条件、复合函数微分法，隐函数及其微分法、二元函数的极值，最大值、最小值及其应用.

(二)考试要求

1.理解二元函数的概念，知道二元函数的几何意义;

2.知道二元函数的极限、连续性等概念以及有界闭域上连续函数的性质;

3.理解偏导数、全微分等概念并熟练掌握其计算，知道全微分存在条件;

4.熟练掌握复合函数的求导法则;

5.会求隐函数所确定的函数的偏导数;

6.理解多元函数极值的概念，会求函数的极值，了解条件极值的概念，会用拉格朗日乘数法求条件极值;

7.会求解一些较简单的最大值和最小值的应用问题。

第八章 二重积分

(一)考试内容

二重积分的的概念及性质，二重积分的计算(直角坐标、极坐标)，二重积分的应用(曲面的面积、体积、薄片质量)。

(二)考试要求

1.理解二重积分的概念，掌握二重积分的性质;

2.熟练掌握直角坐标下二重积分的计算方法;

3.熟练掌握极坐标下二重积分的计算;

4.会应用二重积分求面积，体积、薄片质量。

四、考试方式及时间

1.考试方式：闭卷

2.考试时间：120分钟

五、考试题型结构及分值分布

1. 考试题型结构：单项选择题，填空题，判断题，计算题，证明题。

2. 分值分布：单项选择题(每小题3分，共18分);填空题(每小题4分，共20分);

判断题(每小题2分，共10分);计算题(每小题7分，共42分);证明题(每小题10分，共10分).

六、教材与参考书目

1.黄立宏,彭向阳,杨勇,高等数学[M].上海:复旦大学出版社,2013年.

2.同济大学应用数学系,高等数学[M].北京:高等教育出版社，2014年.

3.汤四平,赵雨清,陈国华,高等数学[M].北京:北京理工大学出版社,2016年.

怀化学院公共数学教研室

　　感谢您阅读2023年怀化学院专升本电气工程及其自动化《高等数学》课程考试大纲，本文出自：诚为径统招专升本网，转载需带上本文链接地址：https://tzzsb.cwjedu.com/ksjc/38392