2023年成都大学专升本高等数学考试大纲
2023年成都大学专升本高等数学考试大纲
Ⅰ. 命题指导思想及原则
命题贯彻党的教育方针,遵循素质教育规律, 落实立德树人根本任务,促进 技术技能人才成长,培养德智体美劳全面发展的社会主义建设者和接班人. 在考 查大学数学的基本概念、基本理论、基本计算的基础上,注重对大学数学基本知 识的运用能力的考查, 坚持多角度、多层次的考查, 体现基础性、综合性、应用 性、创新性。试题应具有较高的信度、效度,必要的区分度和适当的难度.
Ⅱ. 考试范围
考试范围包括《高等数学》和《线性代数》.《高等数学》含函数、极限、 连续、一元函数微分学、一元函数积分学、向量代数与空间解析几何、多元函数 微分学与二重积分、无穷级数、常微分方程等.《线性代数》含行列式、矩阵、 向量、线性方程组等.
Ⅲ. 考试内容及要求
对考试内容的要求由低到高,概念和理论的要求分为 “了解”和“理解”两 个层次;方法和运算的要求分为“会”、“掌握”和“熟练掌握”三个层次.
一、函数、极限和连续
(一)函数
1.理解函数的概念,会求函数的定义域、表达式及函数值。.会求分段函数的定义域、函数值,并会作出简单的分段函数图像。会建立简单实际问题的函数关系式。
2.理解和掌握函数的单调性、奇偶性、有界性和周期性,会判断所给函数的类别。
3.了解函数 之间的关系(定义域、值域、图象),会求单调函数的反函数。
之间的关系(定义域、值域、图象),会求单调函数的反函数。
4.掌握函数的四则运算与复合运算,熟练掌握复合函数的复合过程.
5.熟练掌握基本初等函数的性质及其图象.
6.了解初等函数的概念.
(二)极限
1.了解数列极限的概念,了解数列极限的唯一性、收敛数列的有界性.
2.了解函数极限的概念,理解函数极限存在的充分必要条件,理解函数极 限的唯一性、局部保号性.
3.熟练掌握极限的四则运算法则.
4.了解数列极限的两个收敛准则(夹逼准则与单调有界准则)、函数极限的夹逼准则.熟练掌握两个重要极限.
5.了解无穷小量、无穷大量的概念,掌握无穷小量的性质,掌握无穷小量 与无穷大量的关系. 会比较无穷小量的阶 (高阶、低阶、同阶和等价). 会用等价无穷小量求极限.
(三)连续
1.理解函数在一点连续与间断的概念,会判断函数(含分段函数)的连续 性.
2.会求函数的间断点并判断其类型.
3.理解闭区间上连续函数的有界性定理、最值定理、介值定理,会用零点 存在定理进行证明.
4.了解初等函数在其定义区间上的连续性,会用函数的连续性求极限.
二、一元函数微分学
(一)导数与微分
1.理解导数的概念、导数的几何意义、函数可导性与连续性之间的关系, 会用导数定义判断函数在一点处的可导性.
2.会求曲线的切线方程与法线方程.
3.熟练掌握导数的基本公式、四则运算法则、复合函数的求导法则.
4. 掌握隐函数和由参数方程所确定的函数的求导法, 会用对数求导法, 会 求分段函数的导数.
5.了解高阶导数的概念,会求函数的高阶导数,会求隐函数和由参数方程 所确定的函数的二阶导数.
6.理解函数微分的概念,理解可微与可导的关系,掌握微分的四则运算法 则、一阶微分的形式不变性,会求函数的微分.
(二)微分中值定理与导数的应用
1.理解罗尔中值定理、拉格朗日中值定理,了解它们的几何意义.会用罗尔中值定理和拉格朗日中值定理进行证明.
2.熟练掌握用洛必达法则求“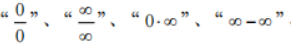 “1”、“0°” 和“∞°”型等未定式的极限。
“1”、“0°” 和“∞°”型等未定式的极限。
3.会用导数判定函数的单调性,掌握函数的单调区间的求法,会用函数的 单调性证明不等式.
4.了解函数极值的概念,掌握函数的极值和最值的求法,会求实际问题的 最值.
5.会判定曲线的凹凸性,会求曲线的凹凸区间和拐点.
6.会求曲线的水平渐近线与垂直渐近线(铅直渐近线).
三、一元函数积分学
(一)不定积分
1.理解原函数与不定积分的概念,掌握不定积分的性质.
2.熟练掌握基本积分公式.
3.熟练掌握不定积分第一换元法,掌握不定积分第二换元法.
4.熟练掌握不定积分的分部积分法.
5.会求有理函数的不定积分.
(二)定积分
1.了解定积分的概念,理解定积分的几何意义,了解函数可积的条件.
2.掌握定积分的基本性质.
3.理解变限积分函数的概念,熟练掌握变限积分函数的导数.
4.熟练掌握牛顿-莱布尼茨公式.
5.熟练掌握定积分的换元积分法与分部积分法.会证明积分等式.
6.了解无穷区间广义积分的概念,掌握其计算方法.
7.掌握直角坐标系下用定积分计算平面图形面积的方法,会求平面图形绕 坐标轴旋转所生成的旋转体体积.
四、向量代数与空间解析几何
(一)向量代数
1.理解向量的概念,掌握向量的坐标表示法,会求单位向量、方向余弦.
2.掌握向量的线性运算、向量的数量积、向量的向量积的计算方法.
3.掌握向量平行、垂直的条件.
(二)平面与直线
1.会求平面的点法式方程、一般式方程.会判定两平面的位置关系.
2.会求点到平面的距离.
3.了解直线的一般式方程,会求直线的对称式方程(点向式方程)、参数 式方程.会判定两直线的位置关系.
4.会判定直线与平面的位置关系.
(三)空间曲面
1. 了解母线平行于坐标轴的柱面的方程及其图形.
2. 了解旋转轴为坐标轴的旋转曲面的方程.
3. 了解球面、椭球面、圆锥面、抛物面的方程及其图形.
五、多元函数微分学与二重积分
(一)多元函数微分学
1.了解多元函数的概念、二元函数的几何意义、二元函数的极限与连续的概念.会求二元函数的定义域.
2.理解偏导数的概念,掌握多元函数的一、二阶偏导数的求法.
感谢您阅读2023年成都大学专升本高等数学考试大纲,本文出自:诚为径统招专升本网,转载需带上本文链接地址:https://tzzsb.cwjedu.com/ksjc/38992
-
 温馨提示:
温馨提示:
- 因考试政策、内容不断变化与调整,诚为径教育网站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
上一篇: 2023年成都大学专升本大学语文考试大纲







