2024年河北省专升本考试高等数学(一)(理工类)专业考试说明

　　(4)理解函数极值的概念，掌握求函数极值的方法，掌握函数最大值、最小值的求法及简单应用。

　　(5)会判断函数图形的凹凸性，会求函数图形的拐点。

　　(6)会求函数图形的水平渐近线和垂直渐近线。

　　(7)会描绘简单函数的图形。

　　三、一元函数积分学

　　(一) 不定积分

　　1.知识范围

　　原函数与不定积分的概念 不定积分的基本性质 基本积分公式 第一换元法(即凑微分法) 第二换元法 分部积分法 简单有理函数、简单无理函数及三角函数有理式的积分。

　　2.考核要求

　　(1)理解原函数与不定积分的概念。

　　(2)理解不定积分的基本性质。

　　(3)掌握不定积分的基本公式。

　　(4)掌握不定积分的第一换元法、第二换元法(限于三角代换与简单的根式代换)和分部积分法。

　　(二)定积分

　　1.知识范围

　　定积分的概念和性质 变上限定积分及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式定积分的换元法和分部积分法 定积分的应用(平面图形的面积，旋转体的体积，物理学中的简单应用) 无穷区间的广义积分的概念与计算。

　　2.考核要求

　　(1)理解定积分的概念，理解定积分的基本性质。

　　(2)理解变上限定积分是其上限的函数及其求导定理，掌握牛顿-莱布尼茨公式。

　　(3)掌握定积分的换元法和分部积分法。

　　(4)掌握用定积分求平面图形的面积、简单的封闭平面图形绕坐标轴旋转所成旋转体体积及定积分在物理学中的简单应用。

　　(5)了解无穷区间的广义积分的概念，会计算无穷区间的广义积分。

　　四、向量代数与空间解析几何

　　(一)向量代数

　　1.知识范围

　　向量的概念 向量的坐标表示 方向余弦 单位向量 向量的线性运算 向量的数量积与向量积及其运算 两向量的夹角 两向量垂直、平行的充分必要条件。

　　2.考核要求

　　(1)理解空间直角坐标系，理解向量的概念及其表示;了解单位向量、向量的模与方向余弦，向量在坐标轴上的投影。

　　(2)掌握向量的线性运算、数量积、向量积，以及用坐标表达式进行向量运算的方法。

　　(3)掌握两向量平行、垂直的条件，会求两向量的夹角。

　　(二)平面与直线

　　1.知识范围

　　平面点法式方程和一般式方程 点到平面的距离 空间直线的标准式(又称对称式或点向式)方程、一般式(又称交面式)方程和参数式方程 直线与直线、直线与平面、平面与平面平行、垂直的条件和夹角。

　　2.考核要求

　　(1)掌握平面的方程，会判定两平面平行、垂直或重合。

　　(2)会求点到平面的距离。

　　(3)掌握空间直线的标准式方程、一般式方程、参数式方程。会判定两直线平行、垂

　　直或重合。

　　(4)会判定直线与平面间的位置关系(垂直、平行、斜交或直线在平面上)。 (三) 曲面的方程

　　1.知识范围

　　曲面方程的概念 球面 母线平行于坐标轴的柱面 旋转轴为坐标轴的旋转曲面 常用二次曲面。

　　2.考核要求

　　(1)了解曲面方程的概念。了解母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程及其图形。

　　(2)了解球面、椭球面、圆柱面、圆锥面和旋转抛物面等常用二次曲面的方程及其图形。

　　五、多元函数微分学

　　1.知识范围

　　多元函数的概念 二元函数的极限与连续的概念 偏导数、全微分的概念 全微分存在的必要条件与充分条件 二阶偏导数 复合函数、隐函数的求导法 偏导数的几何应用 多元函数的极值、条件极值的概念 多元函数极值的必要条件 二元函数极值的充分条件 极值的求法 拉格朗日乘数法。

　　2.考核要求

　　(1)理解多元函数的概念，了解二元函数的几何意义和定义域;了解二元函数极限与连续概念(对计算不作要求)。

　　(2)理解偏导数的概念，了解全微分的概念和全微分存在的必要条件和充分条件。

　　(3)掌握二元初等函数的一、二阶偏导数的计算方法，会求全微分。

　　(4)掌握复合函数一、二阶偏导数的计算方法(含抽象函数)。

　　(5)掌握由方程 F ( x, y)  0 所确定的隐函数 z  z( x, y) 的一阶、二阶偏导数的求法。

　　(6)会求空间曲面的切平面方程和法线方程。

　　(7)会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求二元函数的最大值、最小值并会解一些简单的应用问题。

　　六、多元函数积分学

　　(一)二重积分 1.知识范围

　　二重积分的概念及性质 二重积分的计算 二重积分的几何应用。 2.考核要求

　　(1)理解二重积分的概念，了解其性质。

　　(2)掌握二重积分(直角坐标系，极坐标系)的计算方法。

　　(3)会在直角坐标系内交换两次定积分的次序。

　　(4)会用二重积分求空间曲面所围成立体的体积。

　　(二)曲线积分 1.知识范围

　　对坐标的平面曲线积分的概念及性质 对坐标的平面曲线积分的计算 格林(Green)公式 平面曲线积分与路径无关的条件。

　　2.考核要求

　　(1)理解对坐标的平面曲线积分的概念及性质。

　　(2)掌握对坐标的曲线积分的计算方法。

　　(3)掌握格林公式，会应用平面曲线积分与路径无关的条件。

　　七、无穷级数

　　(一)常数项级数 1.知识范围

　　常数项级数收敛、发散的概念 收敛级数的和 级数收敛的基本性质和必要条件 正项级数收敛性的比较判别法、比值判别法 交错级数的莱布尼茨(Leibniz)判别法 绝对收敛与条件收敛。

　　2.考核要求

　　(1)理解常数项级数收敛、发散以及收敛级数的和的概念。理解级数收敛的必要条件和基本性质。

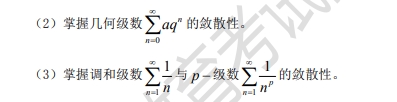
　　(4)掌握正项级数的比值判别法，会用正项级数的比较判别法。

　　(5)会用莱布尼茨判别法判定交错级数收敛。

　　(6)了解级数绝对收敛与条件收敛的概念，会判定任意项级数的绝对收敛与条件收敛。

　　感谢您阅读2024年河北省专升本考试高等数学(一)(理工类)专业考试说明，本文出自：诚为径统招专升本网，转载需带上本文链接地址：https://tzzsb.cwjedu.com/ksjc/60178/p2